Wellenfunktionen lassen sich mit folgender Differentialgleichung sowohl zeitlich, als auch in räumlicher Ausbreitungsrichtung darstellen:
(1)
Eine bekannte Lösung dieser Differentialgleichung ist die harmonische Schwingungsgleichung ebener Wellen. Diese ist wichtig, da jede beliebige Wellenfunktion als Summe von harmonischen Wellenfunktionen dargestellt werden kann und die Summe zweier Lösungen der Differentialgleichung wieder eine Lösung ist.
(2)
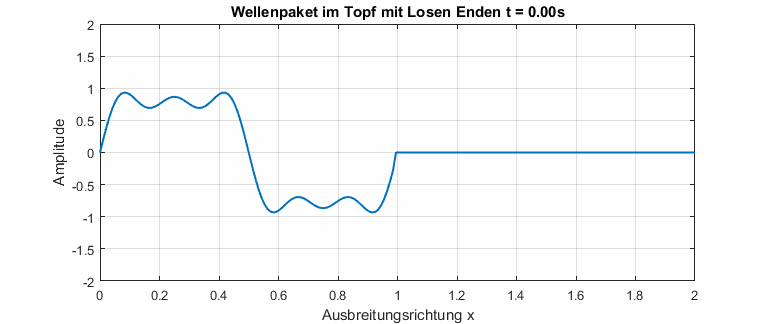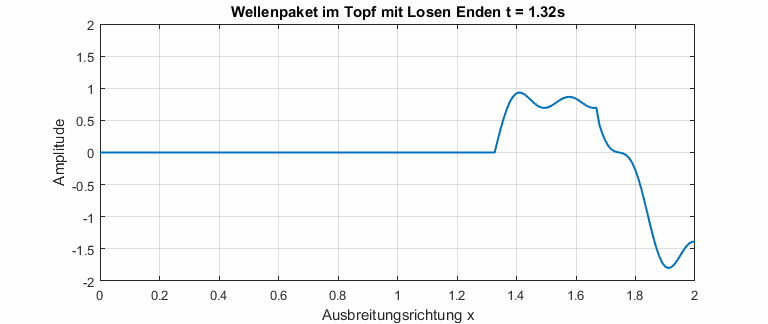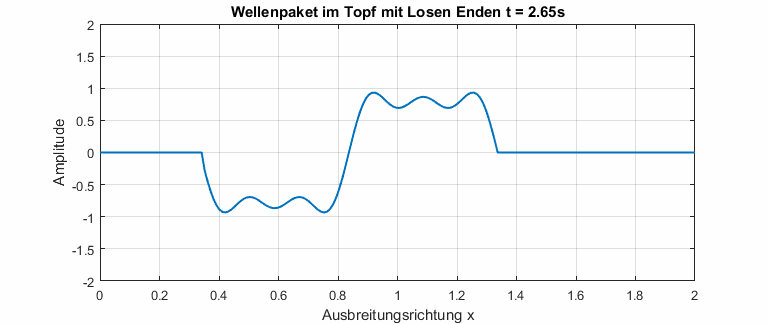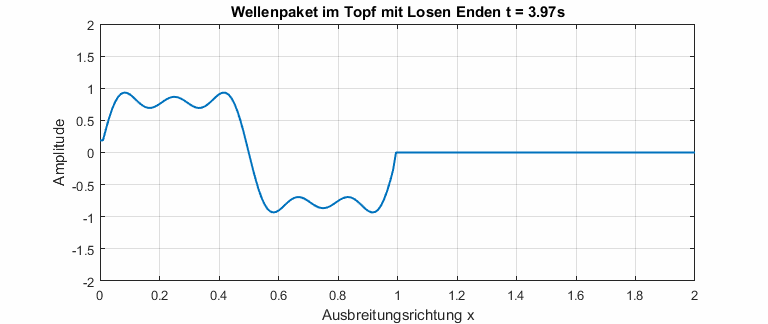
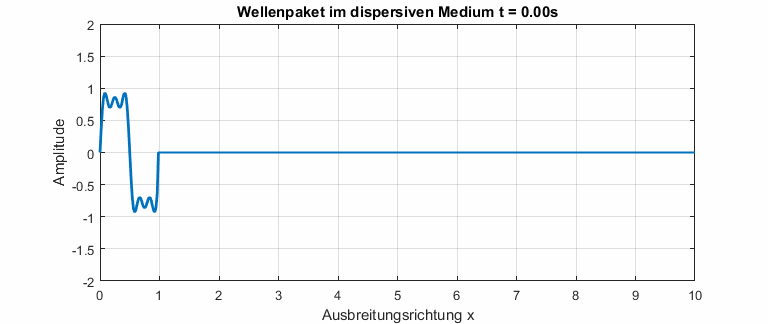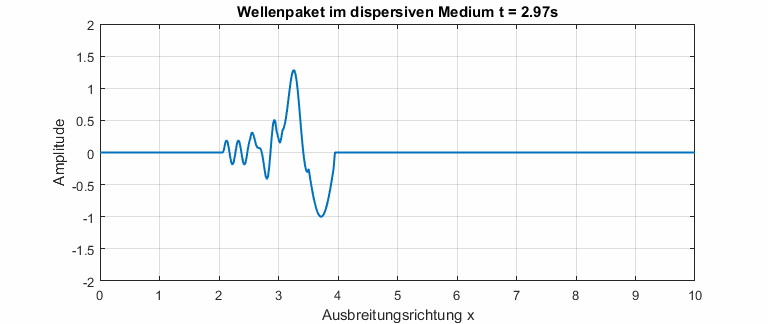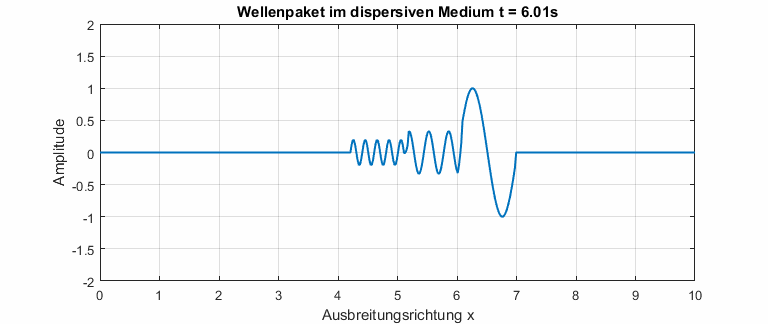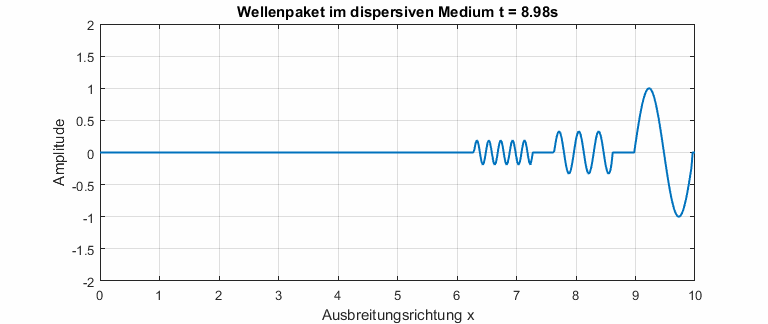
Mit einer numerischen Simulation lässt sich die DGL aus (1) auch mit nicht periodischen Signalen lösen. Zum Beispiel kann ein Wellenpaket, das in einem Topf mit losen Enden gefangen ist, simuliert werden.
In dispersiven Medien ist die Phasengeschwindigkeit abhängig von der Frequenz. Die Dispersionsrelation beschreibt den Zusammenhang zwischen Phasengeschwindigkeit und Frequenz. In der Animation unten ist gut zu erkennen, dass kleine Frequenzen eine höhere Phasengeschwindigkeit haben (Das gilt natürlich nicht allgemein). Das Wellenpaket zerfließt, bis alle Drei Frequenzanteile sichtbar werden.
Die Animationen wurden mit Matlab erstellt. Dabei wurde die DGL aus (1) in eine Differenzengleichung umgeschrieben, um sie numerisch lösen zu können:
(3)
S ist die so genannte Courant Zahl. Wenn S <= 1 ist, dann ist die Differenzengleichung stabil. Damit die Differenzengleichung eine exakte Lösung der DGL liefert, müssen die Zeit- und Wegschritte (
(4) 
